algorithmGenerar Matriz Caracol, Spiral Matrix
Generar una matriz caracol o Spiral Matrix es un problema clásico en programación, especialmente cuando estamos iniciando a utilizar Arrays y una matriz es simplemente un array bidimensional.
Matriz Caracol o Spiral Matrix
Una matriz caracol tiene la forma de su nombre, por ejemplo una matriz cuadrada de tamaño 5 sería la siguiente:
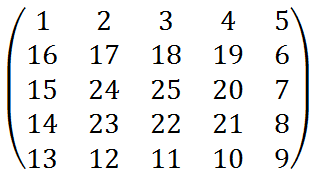
La forma más sencilla de resolverlo es tener cuatro ciclos repetitivos que recorran los lados y uno extra para que repita esa operación en el caso de una dimensión 5 deberá repetirlo 2 veces y colocar un numero mas en el centro, en el caso de dimensión par entonces repetimos dimensión dividido entre 2 veces.
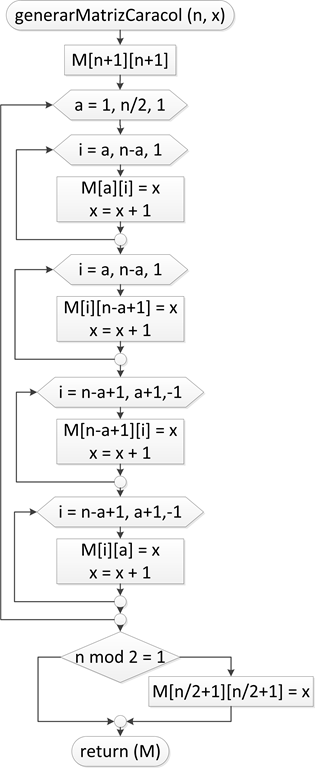
En el diagrama de flujo, n es la dimensión de la matriz cuadrada y x es un número con cual empezara a generar la matriz caracol.
Código
Método que genera la matriz caracol donde n es la dimensión de la matriz (matriz cuadrada) y x es el número por el cual empezará, por ejemplo puedes enviarle 1.
Java
public static int[][] generarMatrizCaracol(int n, int x) {
int[][] M = new int[n + 1][n + 1];
for (int a = 1; a <= n / 2; a++) {
for (int i = a; i <= n - a; i++) {
M[a][i] = x;
x++;
}
for (int i = a; i <= n - a; i++) {
M[i][n - a + 1] = x;
x++;
}
for (int i = n - a + 1; i >= a + 1; i--) {
M[n - a + 1][i] = x;
x++;
}
for (int i = n - a + 1; i >= a + 1; i--) {
M[i][a] = x;
x++;
}
}
if (n % 2 == 1) {
M[n / 2 + 1][n / 2 + 1] = x;
}
return M;
}
Código completo en:
Tomar en cuenta que se genero matriz a partir de la posición (1, 1) sin embargo para la primera posición en Java es (0, 0), podemos cambiar ello de manera sencilla.
Swift
func generateSpiralMatrix(n: Int) -> [[Int]] {
var value = 1
var matrix: [[Int]] = [[Int]](repeating: [Int](repeating: 0, count: n), count: n)
for ring in 0..<(n / 2) {
for i in ring..<(n - ring - 1) {
matrix[ring][i] = value
value += 1
}
for i in ring..<(n - ring - 1) {
matrix[i][n - ring - 1] = value
value += 1
}
for i in ((ring + 1)..<(n - ring)).reversed() {
matrix[n - ring - 1][i] = value
value += 1
}
for i in ((ring + 1)..<(n - ring)).reversed() {
matrix[i][ring] = value
value += 1
}
}
if n % 2 == 1 {
matrix[n / 2][n / 2] = value
}
return matrix
}